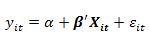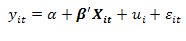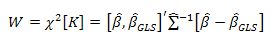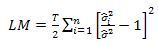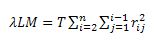PENGUJIAN ASUMSI KLASIK

Penggunaan model analisis regresi berganda terikat dengan sejumlah asumsi dan harus memenuhi asumsi-asumsi klasik yang mendasari model tersebut. Pengujian asumsi yang harus dipenuhi agar Persamaan regresi dapat digunakan dengan baik (uji persyaratan analisis) sebagai berikut:

 Uji Normalitas

Uji normalitas bertujuan untuk menguji apakah dalam model regresi variabel terikat dan variabel bebas keduanya apakah mempunyai distribusi normal atau tidak. Model regresi yang baik harus mempunyai distribusi normal atau mendekati normal (Ghozali 2001). Pengujian dilakukan dengan analisis grafik (scatterplot) yakni dengan melihat normal probability plot yang membandingkan distribusi kumulatif dengan distribusi normal. Distribusi normal akan membentuk satu garis lurus diagonal dan ploting data residual akan dibandingkan dengan garis diagonal. Jika distribusi data residual normal maka garis yang menggambarkan data sesungguhnya akan mengikuti garis diagonalnya.

Uji normalitas lain pada penelitian ini menggunakan uji statistik non parametrik Kolmogorov Smirnov (K-S). Uji K-S dilakukan dengan membuat hipotesis:

Jika nilai Asymp. Sig. (2 – tailed) ≥     0,05  data berdistribusi normal

Jika nilai Asymp. Sig. (2 – tailed) ≥     0,05  data tidak berdistribusi normal.

Uji Autokorelasi

Menurut Imam Ghozali uji autokorelasi bertujuan untuk menguji apakah dalam model regresi linear ada korelasi antara kesalahan pengganggu pada periode t dengan periode t-1 sebelumnya. Jika terjadi korelasi, maka dinamakan problem autokorelasi. Autokorelasi muncul karena observasi yang berurutan sepanjang waktu berkaitan satu sama lain.Masalah ini timbul karena residual (kesalahan pengganggu) tidak bebas dari satu observasi ke observasi lainnya. Pada penelitian ini menggunakan Uji Durbin–Watson (DW test).

Uji Durbin Watson hanya digunakan untuk autokorelasi tingkat satu dan mensyaratkan adanya konstanta dalam model regresi dan tidak ada varibel di antara variabel independen.

Pengambilan keputusan ada tidaknya autokorelasi :

Tabel 3.2

Dasar Pengambilan Keputusan Uji Autokorelasi

Hipotesis nol	Keputusan	Jika
Tidak ada autokorelasi positif	Tolak	0 < d < dl
Tidak ada autokorelasi positif	No decision	dl ≤  d ≤ du
Tidak ada korelasi negatif	Tolak	4- dl < d < 4
Tidak ada korelasi negatif	No decision	4-du ≤ d ≤ 4 - dl
Tidak ada autokorelasi positif atau negatif	Tdk ditolak	du < d < 4 - du

Uji Murtikolinearitas

Menurut Imam Ghozali Uji Multikolonieritas bertujuan untuk menguji apakah model regresi ditemukan adanya korelasi atar variabel bebas (Independent). Model korelasi yang baik seharusnya tidak terjadi korelasi di antara variabel independent. Jika variabel independent saling berkorelasi, maka variabel ini tidak ontogonal. Variabel ontogonal adalah variabel independent yang nilai korelasi antar sesama variabel independent sama dengan nol.

Untuk mendeteksi adanya multikolinieritas dengan membuat hipotesis:

Tolerance  value < 0,10 atau VIF > 10    : terjadi multikolenearitas

Tolerance  value > 0,10 atau VIF < 10    : tidak terjadi multikolenearitas

Uji Heteroskedastisitas

Menurut Imam Ghozali Uji heteroskedastisitas bertujuan untuk menguji apakah dalam model regresi terjadi ketidaksamaan variance dari residual satu pengamatan ke pengamatan lainnya. Penelitian ini menggunakakan Uji Glejser untuk meregres nilai absolut residual terhadap variabel independent (Gujarati, 2003) dengan menggunakan dasar pengambilan keputusan sebagai berikut:

1. Jika  nilai Sig variabel independen < 0,05 terjadi  Heterokedastitas
2. Jika  nilai Sig variabel independen > 0,05 tidak terjadi  Heterokedastitas

Sumber:
Dapat dilihat disini

UJI ASUMSI KLASIK (Analisis Asumsi Klasik Regresi Linier Berganda)

Salah satu analisis yang paling banyak digunakan dalam penelitian adalah regresi linier berganda. yaitu suatu analisis regresi yang mengujikan adanya pengaruh dua atau lebih varibel variabel bebas/ variabel indepen / (variabel x) terhadap satu variabel dependen (Y).

 

Kenapa model regresi lionier lebih banyak dipakai? ada beberapa alasan, salah satu satu model linier merupakan model yang model yang paling model dipahami dibanding teori model nonlinier. selain itu model linier merupakan dasar dari asumsi data normal. namun ternyata pembentukan model linier berganda tidak sesederhana model regresi linier sederhana yang hanya melibatkan satu variabel x kepada satu variabel y.

salah satu kendala besar dalam membentuk model regresi linier berganda adalah adanya 4 asumsi klasik yang harus dipenuhi. secara sederhana, asumsi di sini dapat diartikan sebagai syarat bahwa model regresi yang terbentuk merupakan model yang benar dan bisa dipakai secara tepat. bila ada satu asumsi yang belum lolos alias terkena masalah maka model regresi yang dibuat dapat dikatakn belum bisa mengestimasi pengaruh variabel independen terhadap variabel terikat secara tepat.

 

Asumsi pertama yang pertama adalah, normalitas residual. kesalahan yang biasa terjadi adalah banyak peneliti mengira normalitas yang dimaksud adalah normalitas data, padahal dalam regresi linier normalitas yang dimaksud adalah normalitas residual. setelah menyadari kesalahannya akhirnya peneliti semakin bingung karena untuk menampilkan nilai residual regresi yang dibuat masih bingung...apalagi sampai menguji normalitas. dan paling parahnya setelah bisa menguji normalitas residual , ternyata hasilnya tidak normal. apa yang harus dilakukan agar bisa lolos normalitas?

 

Asumsi regresi kedua, multikolinieritas, multikolinieritas sederhananya adalah menghindari hubungan linier antara variabel independen. sehingga bila ada hubungan linier antara variabel x1 terhadap x2 maka dapat dipastikan model regresi bergandanya akan  bias dan tidak bisa digunakan. pengujian kasus multikolinieritas dapat digunakan nilai VIF. walaupun sederhana, namun masalah ini akan membingungkan ketika terjadi kasus multikolinieritas . secara teoritis, bila terjadi kasus multikolinieritas maka direkomendasikan agar variabel yang multikolinieritas harus dibuang dari model. masalahnya bagaimana bila varaibel yang harus dibuang tersebut adalah variabel yang sangat penting yang tidak mungkin dibuang dari model?

 

Asumsi regresi berganda ketiga adalah autokorelasi, yaitu adanya kondisi dimana terdapat korelasi atau hubungan antar pengamatan (observasi),yaitu  berbentuk observasi deret waktu. Untuk data-data tertentu asumsi autokorelasi bisa disingkirkan dari kewajiban uji. namun yang paling berat adalah bila ternyata terdapat kasus autokorelasi namun terlalu kuat. apa solusinya?

 

Terakhir adalah asumsi heterokedastisitas, yaitu adanya ketidaksamaan varian dari residual untuk semua pengamatan pada model regresi.. menurut saya teknik uji heterokedastisitas yang paling sederhana adalah uji Glejser. bila hasil uji Glejser menunjuka bahwa varian resiudal tidak seragam maka solusi yang bisa dilakukan adalah transformasi seperti transformasi log / ln. namun tidak semua data bisa dilakukan tranformasi seperti data dengan nilai negatif.

 

Solusi apa yang bisa dilakukan untuk data yang tidak lolos asumsi klasik?

secara logika, semakin banyak variabel nbebas x maka semakin sulit model regresi yang tersebut bebas asumsi klasik.

Sumber:
Dapat dilihat disini

UJI ASUMSI KLASIK ( Normalitas, Autokorelasi, Multikolinearitas dan Heteroskedastisitas)

Pengujian Asumsi Klasik Model Regresi Berganda
 1. Uji Asumsi Kalsik Normalitas.

Pengujian asumsi normalitas untuk menguji data variabel bebas (X) dan variabel terikat (Y) pada persamaan regresi yang dihasilkan, apakah berdistribusi normal atau berdistribusi tidak normal. Jika distribusi data normal, maka analisis data dan pengujian hipotesis digunakan statistik parametrik. Pengujian normalitas data menggunakan uji kolmogorov-smirnov one sampel test dengan rumus:

Dimana:
Fo (X) = fungsi distribusi komulatif yang ditentukan.
SN (X) = distribusi frekuensi komulatif yang diobservasi dari suatu sampel random dengan N observasi.
i = 1,2,…N
Adapun kriteria uji : jika probabilitas signifikan > 0,05 maka data berdistribusi normal.

2. Uji Asumsi Klasik Autokorelasi

Persamaan regresi yang baik adalah tidak memiliki masalah autokorelasi. Jika terjadi autokorelasi maka perasamaan tersebut menjadi tidak baik atau tidak layak dipakai prediksi. Ukuaran dalam menentukan ada tidaknya masalah autokorelasi dengan uji Durbin-Watson (DW), dengan ketentuan sebagai berikut:

(a). Terjadi autokorelasi positif jika DW di bawah -2 (DW < -2).
(b). Tidak terjadi autokorelasi jika DW berada di antara -2 dan +2 atau -2 < DW +2.
Berikut langkah prosesnya:
1. Klik menu analyze.
2. Pilih submenu regresion, klik linier.
3. Box dependent: variabel terikat (Y)
4. Box independent: variabel bebas (X)
5. Pada case labels isikan periode waktunya.
6. Klik tombol statistic.
7. Aktifkan durbin-Watson.
8. Klik continue.
9. Klik OK.
Contoh bagian output:

Dari hasil output di atas, Durbin-Watson test = 2,397 dan DW > 2, maka, disimpulkan bahwa data di atas terjadi autokorelasi negatif.

3. Uji Asumsi Klasik Multikolinieritas.

Uji asumsi klasik ini digunakan untuk mengukur tingkat asosiasi (keeratan) hubungan/pengaruh antar variabel bebas tersebut melalui besaran koefisien korelasi (r). Multikolinieritas terjadi jika koefisien korelasi antar variabel bebas lebih besar dari 0,60 (pendapat lain: 0,50 dan 0,90). Dikatakan tidak terjadi multikolinieritas jika koefisien korelasi antar variabel bebas lebih kecil atau sama dengan 0,60 (r < 0,60). Dengan cara lain untuk menentukan multikolinieritas, yaitu dengan :
1. Nilai tolerance adalah besarnya tingkat kesalahan yang dibenarkan secara statistik (a).
2. Nilai variance inflation factor (VIF) adalah faktor inflasi penyimpangan baku kuadarat.

Nilai tolerance (a) dan variance inflation factor (VIF) dapat dicari dengan, sebagai berikut:
☑ Besar nilai tolerance (a): a = 1 / VIF
☑ Besar nilai variance inflation factor (VIF): VIF = 1 / a
~ Variabel bebas mengalami multikolinieritas jika a hitung VIF.
~ Variabel bebas tidak mengalami multikolinieritas jika a hitung > a dan VIF hitung < VIF.
Berikut langkah prosesnya:
1. Klik menu analyze.
2. Pilih submenu regresion, klik linier.
3. Box dependent: variabel terikat (Y)
4. Box independent: variabel bebas (X)
5. Klik method, pilih enter
6. Klik tombol statistic, akan muncul linier regression statistic: nonaktifkan estimates dan model fit, aktifkan: covariance matrix dan collinieritas diagnostics.
7. Klik continue
8. Klik OK.
Contoh bagian output:

Analisis Output:
a). Melihat besaran koefisien korelasi antar variabel bebas, terlihat koefisien korelasi antar variabel bebas sebesar 0,142 jauh di bawah 0,60. Disimpulkan bahwa antara variabel bebas tidak terjadi multikolinieritas.
(b). Menggunakan besaran tolerance (a) dan variance inflation factor (VIF) jika menggunakan alpha/tolerance = 10% atau 0,10 maka VIF = 10. Dari hasil output VIF hitung dari kedua variabel = 1,021 < VIF = 10 dan semua tolerance variabel bebas 0,980 = 98% diatas 10%, dapat disimpulkan bahwa antara variabel bebas tidak terjadi multikolinieritas.

4. Uji Asumsi Klasik Heteroskedastisitas.

Dalam persamaan regresi berganda perlu diuji mengenai sama atau tidak varians dari residual dari observasi yang satu dengan observasi lainnya. Jika residual mempunyai varians yang sama, disebut homoskedastisitas. dan jika varoansnya tidak sama disebut terjadi heteoskedastisitas. Persamaan regresi yang baik jika tidak terjadi heteroskedastisitas.

Analisis uji asumsi heteroskedastisitas hasil output SPSS melalui grafik scatterplot antara Z prediction (ZPRED) untuk variabel bebas (sumbu X=Y hasil prediksi) dan nilai residualnya (SRESID) merupakan variabel terikat (sumbu Y=Y prediksi – Y rill).

Homoskedastisitas terjadi jika titik-titik hasil pengolahan data antara ZPRED dan SRESID menyebar di bawah ataupun di atas titik origin (angka 0) pada sumbu Y dan tidak mempunyai pola yang tertentu.

Heteroskedastisitas terjadi jika pada scatterplot titik-titiknya mempunyai pola yang teratur, baik menyempit, melebar maupun bergelombang-gelombang.
Berikut langkah prosesnya:
1. Klik menu analyze.
2. Pilih submenu regresion, klik linier.
3. Box dependent: variabel terikat (Y)
4. Box independent: variabel bebas (X,…)
5. Klik plots, muncul linier regresion plot dan isikan: variabel SRESID di sumbu Y dan variabel ZPRED di sumbu X.
6. Klik continue.
7. Klik OK.
Contoh bagian output:

Dari hasil output gambar scatterplot, didapat titik menyebar di bawah serta di atas sumbu Y, dan tidak mempunyai pola yang teratur. Maka dapat disimpulakan variabel bebas di atas tidak terjadi heteroskedastisitas atau bersifat homoskedastisitas.

Sumber:
Dapat dilihat disini

PANEL DATA (Sekilas Teori Analisis Regresi Data Panel)

Data Panel adalah gabungan dari data time series dan data cross section, cross section- nya dapat berupa karakteristik suatu perusahaan atau wilayah atau negara. Sehingga dengan menggunakan model regresi data panel dapat dimungkinkan untuk menangkap karakteristik antar individu dan antar waktu yang bisa saja berbeda. Analisis regresi dengan menggunakan data panel mempunyai beberapa keuntungan.

Menurut Hsiao (1992), keuntungan-keuntungan menggunakan analisis regresi data panel adalah:

1. Memperoleh hasil estimasi yang lebih baik karena seiring dengan peningkatan jumlah observasi yang otomatis berimplikasi pada peningkatan derajat kebebasan (degree of freedom);
2. Menghindari kesalahan penghilangan variable (omitted variable problem).

Menurut Baltagi (1995; hlm. 4-7), keuntungan-keuntungan menggunakan analisis regresi data panel antara lain:

1. Mengatasi masalah heterogenitas individu (individual heterogeneity);
2. Memberikan data yang lebih informatif, mengurangi masalah kolinieritas pada variable, mengatasi masalah penghilangan variabel (ommited variabel), dan menghasilkan degree of freedom yang lebih besar;
3. Mempelajari perubahan yang bersifat dinamis (dynamics of adjustment);
4. Dapat mengidentifikasi dan menghitung efek yang tidak dapat dilakukan pada analisis time series atau cross section murni;
5. Dapat mengurangi bias dalam pengestimasian karena data cukup banyak.

Model regresi data panel yang umumnya digunakan terdapat tiga macam, yaitu:

1. Commond Effects Model,
2. Fixed Effects Model (Model Efek Tetap – MET), dan
3. Random Effects Model (Model Efek Random – MER).

1. Commond Effects Model

Merupakan pendekatan model data panel yang paling sederhana karena hanya dengan mengkombinasikan data time series dan cross section dalam bentuk pool, dan menggunakan teknik kuadrat terkecil atau least square untuk mengestimasi koefisiennya. Pada model ini tidak diperhatikan dimensi waktu maupun individu, sehingga diasumsikan bahwa prilaku individu tidak berbeda dalam berbagai kurun waktu.

Persamaan regresinya dapat dituliskan sebagai berikut:

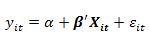
untuk i = 1, 2, …, N dan t = 1, 2, …,T, dimana N adalah jumlah unit/individu cross section dan T adalah jumlah periode waktunya. Dari commond effects model ini akan dapat dihasilkan N+T persamaan, yaitu sebanyak T persamaan cross section dan sebanyak N persamaan time series.

2. Fixed Effects Model

Asumsi pembuatan model yang menghasilkan intersep konstan untuk setiap individu (i) dan waktu (t) dianggap kurang realistik sehingga dibutuhkan model yang lebih dapat menangkap perbedaan tersebut. Model efek tetap (fixed effects), model ini mengasumsikan bahwa perbedaan antar individu dapat diakomodasi dari perbedaan intersepnya. Untuk mengestimasi model Fixed Effects dengan intersep berbeda antar individu, maka digunakan teknik variable dummy. Model estimasi ini sering juga disebut dengan teknik Least Squares Dummy Variable (LSDV).

Persamaan regresinya adalah sebagai berikut:

untuk i = 1,2, …, N dan t = 1,2, …, T, dimana N adalah jumlah unit/individu cross section dan T adalah jumlah periode waktunya.

3. Random Effects Model

Di dalam mengestimasi data panel dengan model Fixed Effects melalui teknik LSDV  menunjukkan ketidakpastian model yang digunakan. Untuk mengatasi masalah ini kita bisa menggunakan variabel residual yang dikenal sebagai model Random Effects. Pada model ini, akan dipilih estimasi data panel dimana residual mungkin saling berhubungan antar waktu dan antar individu. Oleh karena itu, pada model ini diasumsikan bahwa ada perbedaan intersep untuk setiap individu dan intersep tersebut merupakan variabel random atau stokastik. Sehingga dalam model ini terdapat dua komponen residual, yaitu residual secara menyeluruh, yang merupakan kombinasi time series dan cross section, dan residual secara individu yang merupakan karakteristik random dari observasi unit ke-i dan tetap sepanjang waktu.

Adapun persamaan regrsinya adalah sebagai berikut:

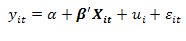
Ada beberapa asumsi yang harus dipenuhi dalam model efek random. Secara matematis, asumsi tersebut terdiri dari:

Hal ini berarti bahwa komponen error tidak berkorelasi satu sama lain dan tidak ada autokorelasi antara cross section dan time series. metode OLS tidak bisa digunakan untuk mendapatkan estimator yang efisien. Metode yang tepat untuk mengestimasi model random effects adalah Generalized Least Squares (GLS) dengan asumsi homoskedastik dan tidak ada cross sectional correlation. GLS merupakan OLS dengan transformasi variabel yang memenuhi asumsi standar dari OLS.

Pemilihan Model Regresi Data Panel

Dari ketiga model yang telah dijelaskan sebelumnya, maka selanjutnya akan ditentukan model yang paling tepat untuk mengestimasi parameter regresi data panel. Secara informal, ada beberapa pertimbangan untuk menentukan model estimasi terbaik dari ketiga model estimasi data panel sebagaimana telah dijelaskan di atas. Nachrowi dan Usman (2006) menyatakan bahwa jika data panel yang dimiliki mempunyai waktu (T) lebih besar dibandingkan dengan jumlah individu (N) maka disarankan untuk menggunakan model fixed effects, sedangkan apabila jumlah data panel yang dimiliki mempunyai jumlah waktu (T) lebih kecil disbanding jumlah individu (N) maka disarankan menggunakan model random effects.

Secara formal terdapat tiga pengujian yang digunakan untuk memilih model regresi data panel terbaik antara model commond effects, model fixed effects, atau model random effectss, yaitu uji F yang digunakan untuk memilih antara model commond effectss atau model fixed effects; uji Lagrange Multiplier (LM) untuk memilih antara model commond effects atau model random effects; dan uji Hausman untuk memilih antara model fixed effects atau model random effects. Adapun penjelasan mengenai ketiga pengujian tersebut di atas adalah sebagai berikut:

Pengujian Signifikansi Model Fixed Effects

Signifikansi model fixed effects dapat dilakukan dengan uji statistik F. Uji F digunakan untuk mengetahui apakah teknik regresi data panel dengan fixed effects lebih baik dari model regresi data panel tanpa variabel dummy (common effects) dengan melihat residual sum of squares (RSS). Hipotesis nol (H₀) yang digunakan adalah bahwa intersep dan slope adalah sama.

Adapun uji F statistiknya adalah sebagai berikut:

dengan n = jumlah individu; T = jumlah periode waktu; K = banyaknya parameter dalam model fixed effects;  dan  masing-masing merupakan residual sum of squares teknik tanpa variabel dummy dan teknik fixed effects dengan variabel dummy. Nilai statistik  F akan mengikuti distribusi statistik F dengan derajat bebas (dof) sebesar/sebanyak n-1 untuk numerator dan sebesar nT-k untuk denumerator. Jika nilai statistik  F lebih besar dari nilai F table pada tingkat signifikansi tertentu, maka hipotesis nol akan ditolak, yang berarti asumsi koefisien intersep dan slope adalah sama tidak berlaku, sehingga teknik regresi data panel dengan fixed effects lebih baik dari model regresi data panel tanpa variabel dummy atau common effects.

Pengujian Signifikansi Model Random Effects

Untuk mengetahui apakah model Random Effects lebih baik daripada model common effects maka dapat menggunakan uji Lagrange Multiplier (LM) yang dikembangkan oleh Bruesch-Pagan. Pengujian ini didasarkan pada nilai residual dari model common effects.Hipoesis yang diajukan adalah intersep bukan merupakan variabel random atau stokastik. Dengan kata lain varian dari residual pada persamaan (3-3) bernilai nol.

Adapun nilai statistik LM dihitung berdasarkan formula sebagai berikut:

di mana n = jumlah individu; T = jumlah periode waktu dan  adalah residual metode common effects (OLS). Uji LM ini didasarkan pada distribusi chi-square dengan derajat bebas sebesar 1. Jika hasil statistik LM lebih besar dari nilai kritis statistik chi-square, maka hipotesis nol akan ditolak, yang berarti estimasi yang tepat untuk regresi data panel adalah metode random effects daripada metode common effects.

Pengujian Signifikansi Model Fixed Effects atau Model Random Effects

Untuk mengetahui apakah model fixed effect lebih baik dari model random effect, digunakan uji Hausman. Dengan mengikuti kriteria Wald, nilai statistik Hausman ini akan mengikuti distribusi chi-square sebagai berikut:

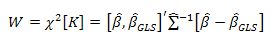
Statistik uji Hausman ini mengikuti disribusi statistik chi-square dengan derajat bebas sebanyak jumlah variabel independen (p). Hipotesis nol ditolak jika nilai statistik Hausman lebih besar daripada nilai kritis statistik chi-square . Hal ini berarti bahwa model yang tepat untuk regresi data panel adalah model Fixed Effects daripada model Random Effects.

Pemilihan Model Estimator Terbaik dari Model Regresi Data Panel Terpilih

Untuk mendapatkan estimator terbaik dari model regresi data panel terpilih, dilakukan pengujian terhadap struktur kovarians dari residual model terpilih. Terdapat beberapa metode yang sesuai dengan asumsi pada stuktur varians-covarians tersebut, yaitu struktur homoskedastik, asumsi struktur heteroskedastik dan tidak ada korelasi antar individu (cross sectional correlation), asumsi heteroskedastik dan ada cross sectional correlation (Seemingly Uncorrelated Regression/SUR), dan asumsi adanya autokorelasi antar waktu pada error term.

 Pemilihan Estimator Asumsi Homoskedastis atau Heteroskedastis

Pada pengujian ini, hipotesis nol (H₀) yang digunakan adalah bahwa struktur varians-covarians residual bersifat homoskedastik. Sementara hipotesis alternatifnya adalah struktur varians-covarians residual bersifat heteroskedastik. Secara matematis, statistik uji yang digunakan dapat dirumuskan sebagai berikut:

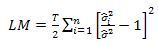
di mana T adalah jumlah observasi, n adalah jumlah individu,  sigma kuadrat i adalah varians residual persamaan ke-i pada kondisi homoskedastik, dan  sigma kuadrat adalah sum square residual persamaan systempada kondisi homoskedasik.Statistik uji LM ini mengikuti distribusi statistik chi-square dengan derajat bebas sebanyak n-1. Jika nilai statistik LM lebih besar dari nilai kritis statistik chi-square, maka hipotesis nol akan ditolak, yang berarti struktur varians-covarians residual bersifat homoskedastik. Prosedur yang digunakan dalam pengolahan dengan Eviews adalah no-weight.

Pemilihan Estimator Asumsi Heteroskedastis Tanpa Korelasi Antar Individu atau Heteroskedastis Ada Korelasi Antar Individu.

Pengujian ini dilakukan apabila hasil pengujian LM pada poin (a) menunjukkan bahwa struktur varians-covarians residual bersifat heteroskedastik. Pada pengujian ini, hipotesis nol (H₀) yang digunakan adalah bahwa struktur varians-kovarians residual bersifat heteroskedastik dan tidak ada korelasi antar individu (non cross sectional correlation). Sementara hipotesis alternatifnya (H₁) adalah bahwa struktur varians-kovarians residual bersifat heteroskedastik dan ada ada korelasi antar individu (cross sectional correlation) atau Seemingly Uncorrelated Regression/SUR.

Secara sistematis, statistik uji yang digunakan dapat dirumuskan sebagai berikut:

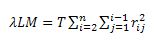
dimana  r-square adalah residual correlation coefficient. Statistik uji  ini mengikuti distribusi statistik chi-square dengan derajat bebas sebanyak n(n-1)/2. Jika nilai statistik observasi lebih besar dari nilai kritis statistik chi-square, maka hipotesis nol akan ditolak, yang berarti struktur varian-kovarians residual bersifat heteroskedastik dan ada korelasi antar individu (cross sectional correlation) atau Seemingly Uncorrelated Regression/SUR. Dengan demikian prosedur yang digunakan dalam Eviews adalah cross-section SUR sedangkan jika hipotesis nol tidak ditolak, prosedur yang digunakan adalah cross-section weights.

Untuk mengestimasi parameter dalam model dapat menggunakan bantuan software EViews 6.0

Semoga bermanfaat d(^.^)b

Sumber:

Dapat dilihat disini

PANEL DATA (PENGUJIAN SIGNIFIKANSI FIXED EFFECT MODEL) (2)

Materi Pengujian Signifikansi Fixed Effects Model…  

Pengujian Signifikansi Fixed Effects Model bertujuan untuk memperbandingkan antara model Fixed Effects dengan model common Effects, dimana hipotesis Null nya adalah model common effects lebih baik, artinya memang tidak ada perbedaan efek antar individu (waktu kalau menggunakan efek fixed period) pada data panel.

Tahapan Pengujiannya adalah sebagai berikut:

1. Model telah dilakukan Estimasi terlebih dahulu, misalnya Fixed effect pada cross-section nya, seperti yang telah dilakukan pada saat materi Estimasi data panel menggunakan E-views (silahkan dilihat kembali).

2. Pada saat ingin menguji Signifikansi Fixed Effects Model, pastikan kembali bahwa estimation method yang digunakan cross section/period nya tertulis Fixed, kemudian OK.

3.  Pada Pool, pilih VIEW à Fixed/Random Effect Testing à Redundant Fixed Effect – Likelihood Ratio , Kemudian Klik

 

 
4.  Kemudian akan muncul Output seperti ini:

 

Seperti yang dapat dilihat pada output diatas, nilai Prob=0.0000 untuk Cross-section F, yang berarti kurang dari 0.05 (KEPUTUSAN: TOLAK Ho) sehingga dapat disimpulkan dengan tingkat keyakinan 95 persen model FIXED Effects lebih baik daripada model COMMON Effects.
Atau penghitungan Semi manualnya dapat dilakukan sebagai berikut:
1. Cari Sum Square Residual Model Common à RSS 1 dengan cara method estimasinya tidak dirubah menjadi fixed ataupun common (Lihat Estimasi data panel menggunakan E-views).

 

2. Cari Sum Square Residual Model Fixed à RSS 2 dengan cara method estimasi nya dirubah menjadi Fixed (Lihat Estimasi data panel menggunakan E-views).

 

3.   Lakukan Penghitungan sesuai dengan rumus pada Pengujian signifikansi Fixed Effects Model. 
Disini saya menggunakan bantuan program Ms. Excell untuk menghitungnya.

Kesimpulan yang diperoleh sama saja, karena memang ini hanya penjabaran rumusnya saja… Terimakasih telah membaca…

Sumber:

Blog F. Fadly

PANEL DATA (Pengujian Signifikansi Random Effects (Common versus Random Effects)

 

Sumber:
Dapat dilihat disini

PANEL DATA (Pengujian Signifikansi Model Fixed Effects)

 

Sumber:
Dapat dilihat disini

PANEL DATA (Cara Import & Estimasi Regresi Data Panel)

Disini akan coba saya sampaikan secara singkat dan dalam tempo yang sesingkat-singkatnya…Lho…hahaha?? Sebenarnya pada Eviews sendiri banyak teknik untuk mengentri data, bisa secara langsung(Manual) ataupun dengan cara import data dari Ms. Excell. Namun khusus untuk data panel saya biasa melakukan import langsung dari Ms. Excell karena lebih cepat dan lebih mudah daripada input manual pada Eviews. Pada Eviews 6 yang saya gunakan, saya biasa mengimport  file Ms.Excell yang sudah berformat tahun 2003-2007.

Tahapan-tahapan import data panel dari Ms. Excell (Tersedia versi video disini) adalah sebagai berikut:

1. Siapkan file Ms. Excell yang akan diimport, Simpan dalam format .XLS (format 2003-2007). Perhatikan susunan tabelnya. Provinsi i kemudian periode (t) nya bergerak, setelah selesai baru dilanjutkan kepada provinsi berikutnya begitu seterusnya. Contoh formatnya adalah sebagai berikut:

Data yang digunakan pada simulasi ini adalah data 30 provinsi yang diamati dalam rentang waktu 2006-2008, variabelnya dimisalkan saja Y, X1, X2 dan X3, seperti yang terlihat dibawah ini.

Setelah disimpan file Ms. Excell 2003-2007 nya jangan lupa ditutup filenya (atau save as ke format yang berbeda dari Ms. Excell yang akan diinput)

2.      Bukalah Eviews yang anda miliki, Kemudiaan pilih file >new >workfile

3.      Karena menggunakan data tahunan, maka frekuensinya dalam annual, dimulai dari tahun 2006-2008. OK

4.      Kemudian pada workfile, klik Object >New Object >Pool > tuliskan nama pool nya misal FERDI

Kemudian pada pool, identifikasikan observasi kita, tetapi dahulukan dengan menggunakan “_”, bisa berupa angka, bisa berupa tulisan, misalnya: _1,_2,…,_30 ataupun _NAD,_SUMUT,…,_PAPUA

5.      Setelah identifikasi, pilih opsi proc > import pool data

6.      Pada upper left data, isikan pada cell apakah input data dimulai (misal D2), kemudian identifikasi variabel yang digunakan (Note: akhiri identifikasi variabel dengan tanda tanya ?)

7.      Apabila input data panel benar, maka akan terbentuk data input pada workfile yang ditandai dengan x1_1 sampai x1_30, hingga y_1 sampai y_30

Note: Cek terlebih dahulu, apakah data sudah benar, apabila ada nilai yang tertukar, itu artinya kita salah dalam penyusunan tabel yang akan diinput pada Ms. Excell, perbaiki format struktur tabelnya (Back to Tahapan 1).

8.      Lakukan estimasi model sederhana. Caranya pada workfile klik pool Ferdi, kemudian pada pool pilih estimate.

Dependent Variable, isikan dengan y? (jangan lupa tanda tanya ya). Kemudian untuk Independent Variable nya, diisikan juga variabel nya dan jangan lupa diakhiri tanda tanya.

9.      Kemudian pada model estimasi nya dapat ditentukan apakah menggunakan fixed effects model ataupun random effects model.

Note: ada pilihan cross section dan ada pilihan period, coba baca kembali introduction dan model estimasi.

10.  Dan inilah hasil outputnya

Dimana ditunjukkan dari nilai Prob (f-stat) yang kurang dari 0.1 (sebagai overall test) bahwa dengan tingkat keyakinan 90 persen, minimal ada satu variabel yang berpengaruh signifikan terhadap variabel tidak bebas. Variabel yang signifikan ditandai oleh prob t-statistik (sebagai partial test) yang kurang dari 0.1. Sehingga dengan tingkat keyakinan 90 persen variabel yang signifikan mempengaruhi Y adalah variabel X1 dan X3. Dan model dapat menjelaskan 97,7 persen variasi yang terjadi pada variabel y (adjusted R-squared).

Sekian penjelasan Cara Mengimport dan Estimasi Regresi data panel dari file Ms. Excell, semoga bermanfaat.

Sumber:
Dapat dilihat disini

PANEL DATA [Tutorial E-views] Hausmann Test

Nah untuk pengujian hausmann, yang teman-teman harus pastikan adalah sedang dalam kondisi model random effects.

3.      Pilih view > Fixed/Random Effect Testing > Correlated Random Effects – Hausmann Test

4.      Berikut hasil Output nya

Nilai Prob yang besar dari 0.05 menunjukkan kondisi terima Ho. Dalam hal ini Ho nya adalah Model random lebih baik dibandingkan model Fixed Effect. Sehingga karena nilai prob nya = 0.5682, maka dengan tingkat keyakinan 95% dapat disimpulkan bahwa untuk data yang kita miliki model random effect lebih sesuai digunakan. Mungkin ini dulu, lain kesempatan saya akan menulis kembali. Terimakasih.

Sumber:
Dapat dilihat disini

PANEL DATA [Tutorial E-views] Pengujian Signifikansi Fixed Effects Model

Tahapan Pengujiannya adalah sebagai berikut :

1.      Model telah dilakukan Estimasi terlebih dahulu, misalnya Fixed effect pada cross-section nya, seperti yang telah dilakukan pada saat materi Estimasi data panel menggunakan E-views (silahkan dilihat kembali).

2.      Pada saat ingin menguji signifikansi Fixed Effects Model, pastikan kembali bahwa estimation method yang digunakan cross section/period nya tertulis Fixed, kemudian OK.

3.      Pada Pool, pilih VIEW à Fixed/Random Effect Testing à Redundant Fixed Effect – Likelihood Ratio , Kemudian Klik

4.      Kemudian akan muncul Output seperti ini:

Seperti yang dapat dilihat pada output diatas, nilai Prob=0.0000 untuk Cross-section F, yang berarti kurang dari 0.05 (KEPUTUSAN: TOLAK Ho) sehingga dapat disimpulkan dengan tingkat keyakinan 95 persen model FIXED Effects lebih baik daripada model COMMON Effects.

            Atau penghitungan Semi manualnya dapat dilakukan sebagai berikut :

1.      Cari Sum Square Residual Model Common à RSS 1 dengan cara method estimasi nya tidak dirubah menjadi fixed ataupun common (Lihat Estimasi datapanel menggunakan E-views).

2.      Cari Sum Square Residual Model Fixed à RSS 2 dengan cara method estimasi nya dirubah menjadi Fixed (Lihat Estimasi data panel menggunakan E-views).

3.   Lakukan Penghitungan sesuai dengan rumus pada Pengujian signifikansi Fixed Effects Model.

Disini saya menggunakan bantuan program Ms. Excell untuk menghitungnya

            Kesimpulan yang diperoleh sama saja, karena memang ini hanya penjabaran rumusnya saja… Terimakasih telah membaca…

Sumber:
Dapat dilihat disini